monad

注意： 这是关于从头开始学习JavaScript ES6 +中的函数式编程和组合软件技术的“Composing Software”系列（现在是一本书！）的一部分。敬请关注。还有更多这方面的内容！ <上一页| <<从第1部分开始

在你开始学习monads之前，你应该已经知道了：

  • 函数组合: compose(f, g)(x) = (f ∘ g)(x) = f(g(x))

  • Functor基础: 了解Array.map操作。

“一旦你了解了monad，你就会立刻无法向其他任何人解释”Monadgreen夫人的咒骂~Gilad Bracha（道格拉斯·克罗克福德着名）

“博士Hoenikker曾经说过，任何无法向八岁的孩子解释他在做什么的科学家都是骗子。“~Kurt Vonnegut的小说”猫的摇篮“

如果你去互联网搜索“monad”，你会被难以理解的类别理论数学和一群人“帮助”解释墨西哥卷饼和太空服的monads。

Monads很简单。行话很难。让我们切入本质。

monad 是一种组合函数的方法，除了返回值之外还需要上下文，例如计算，分支或I / O。Monads类型提升(lift)，展平(flatten)和映射(map)，以便类型排列提升功能a => M（b），使它们可组合。它是从某种类型a到某种类型b的映射以及一些计算上下文，隐藏在lift，flatten和map的实现细节中：

  • 函数map: a => b

  • 防函数(Functors) map及上下文 : Functor(a) => Functor(b)

  • Monads flatten and map及上下文: Monad(Monad(a)) => Monad(b)

但是啊，flatten(展平), map(映射)和context(上下文)意味着什么意思呢？

  • Map map的意思是“将函数应用于a然后返回b”。给定一些输入，返回一些输出。

  • Context 上下文是monad组合的计算细节（包括提升(lift)，展平(flatten)和映射(map)）。Functor / Monad API及其工作提供了上下文，允许将monad与应用程序的其余部分组合在一起。仿函数(fuctor)和monad的观点是将这种背景抽象出去，这样我们在编写东西时就不必担心它了。在上下文中的映射意味着将函数从a=> b应用于上下文中的值，并返回包含在同一类上下文中的新值b。左边的可观测量？右侧的观测量: Observable(a) => Observable(b)。左侧的数组？右侧的数组：Array(a) => Arra(b)。

  • Type lift 类型提升意味着将类型提升到上下文中，使用可用于从该值计算的API来祝福该值，触发上下文计算等... 。a => F(a)（Monads是一种functor(仿函数)）。

  • Flatten 展平意味着从上下文中展开值。 F(a) => a。

看下面的这个例子：

const x = 20;             // Some data of type `a`
const f = n => n * 2;     // A function from `a` to `b`
const arr = Array.of(x);  // The type lift.
// JS has type lift sugar for arrays: [x]
// .map() applies the function f to the value x
// in the context of the array.
const result = arr.map(f); // [40]

在这种情况下，Array是上下文，x是我们映射的值。

此示例不包含二维数组，但可以使用.concat()在JS中展平数组：

[].concat.apply([], [[1], [2, 3], [4]]); // [1, 2, 3, 4]

或许你早就已经在使用monads

无论你的技能水平或对类别理论的理解如何，使用monads都可以使你的代码更易于使用。未能利用monad可能会使你的代码更难处理（例如，回调地狱，嵌套条件分支，更多冗长）。

请记住，软件开发的本质是组合，monad使组合更容易。再看看monad是什么的本质：

  • 函数映射(functions map)：a => b，它允许你组成a => b类型的函数。

  • 伪函数映射以及上下文(Functors map with context): Functor(a) => Functor(b)可以让你组合函数F(a) => F(b)

  • Monads flatten,map和context: Monad(Monad(a)) => Monad(b)可以让你组合提升函数: a => F(b)

这些只是表达函数组合 的不同方式。函数存在的整体原因是你可以编写组合它们。函数可以帮助你将复杂问题分解为更容易单独解决的简单问题，以便你可以通过各种方式组合它们来构建应用程序。

理解功能及其正确使用的关键是对函数组合的更深入理解。

函数组合创建数据流经的函数管道。你在管道的第一阶段输入了一些输入，并且一些数据从管道的最后一个阶段弹出，进行了转换。但要实现这一点，管道的每个阶段都必须期望前一阶段返回的数据类型。

编写简单的函数很容易，因为类型都很容易排列。需将输出类型b与输入类型b匹配即可开展业务：

g:           a => b
f:                b => c
h = f(g(a)): a    =>   c

如果要映射F(a) => F(b)，那么使用仿函数进行组合也很容易，因为类型排列：

g:             F(a) => F(b)
f:                     F(b) => F(c)
h = f(g(Fa)):  F(a)    =>      F(c)

但是如果你想从a => F(b)，b => F(c)等组成函数，你需要monad。让我们将F()交换为M()以使其清楚:

g:                  a => M(b)
f:                       b => M(c)
h = composeM(f, g): a    =>   M(c)

哎呀。在此示例中，组件函数类型不对齐！对于f的输入，我们期望是类型b，但是我们得到的却是M(b)(b的monad)。因为这个错位，composeM()需要散开g返回的M(b)，这样我们就可以将它传递给f，因为f期望类型为b，而不是类型M(b)。该过程（通常称为.bind()或.chain()）是flatten和map发生的地方。

它在传递给下一个函数之前将其从M(b)中展开b，从而导致：

g:             a => M(b) flattens to => b
f:                                      b           maps to => M(c)
h composeM(f, g):
               a       flatten(M(b)) => b => map(b => M(c)) => M(c)

Monads使类型排列为提升函数a => M(b)，以便可以组合它们。

在上图中，M(b) => b的展平和b => M(c)的映射在a => M(c)的链内发生。链调用在composeM()中处理。在较高的层面上，你不必担心它。你可以使用与用于组成常规函数的相同类型的API来组合monad-returns函数。

需要Monad，因为许多函数不是来自a => b的简单映射。有些函数需要处理副作用（promises，streams），处理分支（Maybe），处理异常（Either）等等......

下面是一个更具体的例子。如果你需要从异步API中获取用户，然后将该用户数据传递给另一个异步API以执行某些计算，该怎么办？

getUserById(id: String) => Promise(User)
hasPermision(User) => Promise(Boolean)

让我们写一些函数来演示这个问题。首先，实用程序，compose()和trace()：

const compose = (...fns) => x => fns.reduceRight((y, f) => f(y), x);
const trace = label => value => {
  console.log(`${ label }: ${ value }`);
  return value;
};

然后一些函数去组合(不了解的可以看我之前的一篇文章)

{
  const label = 'API call composition';
  // a => Promise(b)
  const getUserById = id => id === 3 ?
    Promise.resolve({ name: 'Kurt', role: 'Author' }) :
    undefined
  ;
  // b => Promise(c)
  const hasPermission = ({ role }) => (
    Promise.resolve(role === 'Author')
  );
  // Try to compose them. Warning: this will fail.
  const authUser = compose(hasPermission, getUserById);
  // Oops! Always false!
  authUser(3).then(trace(label));
}

当我们尝试组合hasPermission()和getUserById()生成了authUser(), 我们进入了一个大的问题中。因为hasPermission()会期待一个User对象并且得到Promise(User)去代替。为了解决这个问题，我们需要composePromises()去换掉compose() - 一个特殊版本的compose知道它需要使用.then来完成函数组合：

{
  const composeM = chainMethod => (...ms) => (
    ms.reduce((f, g) => x => g(x)[chainMethod](f))
  );
  const composePromises = composeM('then');
  const label = 'API call composition';
  // a => Promise(b)
  const getUserById = id => id === 3 ?
    Promise.resolve({ name: 'Kurt', role: 'Author' }) :
    undefined
  ;
  // b => Promise(c)
  const hasPermission = ({ role }) => (
    Promise.resolve(role === 'Author')
  );
  // Compose the functions (this works!)
  const authUser = composePromises(hasPermission, getUserById);
  authUser(3).then(trace(label)); // true
}

我们稍后会介绍composeM正在做什麽。

记住monad的精髓：

  • 函数映射: a => b

  • 伪函数映射和上下文: Functor(a) => Functor(b)

  • Monad的展平，映射和上下文：Monad(Monad(a)) => Monad(b)

在这种情况下，我们的monad确实是promises，所以当我们编写这些promise-returns函数时，我们有一个Promise(User)而不是hasPermission()所期望的User。注意，如果你从Monad(Monad(a))中取出外部Monad()包装器，你将留下Monad(a) => Monad(b)，它只是常规的仿函数.map。如果我们有一些可能使Monad(x) => x变平的东西，那么我们就会开展业务。

Monad是做什么的

monad基于简单的对称性 - 将值包装到上下文中的方法，以及从上下文中解包值的方法：

  • Lift/unit 从某种类型升级到monad环境中的类型：a => M(a)

  • Flatten/Join: 从上下文中展开类型：M(a) => a

由于monad也是仿函数(functor)，他们也可以映射:

  • Map: 保留上下文的映射 M(a) -> M(b)

结合flatten和map,你会得到一个chain(链) — 用于monad-lifting函数的函数组合，又名Kleisli组合，以Heinrich Kleisli命名：

  • FlatMap/Chain: Flatten + map: M(M(a)) => M(b)

对于monad，map方法通常会在公开的API中省略。Lift + flatten没有明确说明.map，但你拥有制作它所需的所有成分。如果你可以提升（也就是/ unit）和链（又名bind / flatMap），你可以制作.map：

const MyMonad = value => ({
  // <... insert arbitrary chain and of here ...>
  map (f) {
    return this.chain(a => this.constructor.of(f(a)));
  }
});

因此，如果为monad定义.of和.chain/.join，则可以推断出.map的定义。

Lift是工厂/构造函数和/或constructor.of方法。在范畴理论中，它被称为“单位”。它所做的只是将类型提升到monad的上下文中。它将a变成a的Monad。

在Haskell中，它（非常令人困惑）称为return，当你试图大声谈论它时会非常混乱，因为几乎每个人都将它与函数返回混淆。我几乎总是称它为散文中的“lift”或“type lift”，以及代码中的.of。

这种展平过程（没有.chain中的map）通常称为flatten或join。经常（但不总是），flatten/ join被完全省略，因为它内置在.chain/.flatMap中。展平通常与构图相关联，因此它经常与mapping相结合。请记住，解包+map都需要组成a=> M(a)函数。

根据正在处理的monad类型，展开过程可能非常简单。在身份monad的情况下，它就像.map，除了你不将结果值提升回monad上下文。这具有丢弃一层包装的效果：

{ // Identity monad
const Id = value => ({
  // Functor mapping
  // Preserve the wrapping for .map() by 
  // passing the mapped value into the type
  // lift:
  map: f => Id.of(f(value)),
  // Monad chaining
  // Discard one level of wrapping
  // by omitting the .of() type lift:
  chain: f => f(value),
  // Just a convenient way to inspect
  // the values:
  toString: () => `Id(${ value })`
});
// The type lift for this monad is just
// a reference to the factory.
Id.of = Id;

但是，解包部分也是副作用，错误分支或等待异步I/O等奇怪的东西通常隐藏的地方。在所有软件开发中，组合是所有真正有趣的东西发生的地方。例如，使用promises，.chain调用.then。调用promise.then(f)不会立即调用f()。相反，它将等待承诺解析，然后调用f()（因此名称）。

看下面的例子啊:

{
  const x = 20;                 // The value
  const p = Promise.resolve(x); // The context
  const f = n => 
    Promise.resolve(n * 2);     // The function
  const result = p.then(f);     // The application
  result.then(
    r => console.log(r)         // 40
  );
}

使用promises，使用.then代替.chain，但它几乎是一样的。

可能听说过承诺并非严格意义上的monad。那是因为如果值是一个开头的承诺，它只会打开外部承诺。否则，.then的行为类似于.map。

但是因为它对promise值和其他值的行为不同，所以.then并不严格遵守所有函子和/或monad必须满足所有给定值的所有数学定律。在实践中，只要知道该行为分支，通常可以将它们视为。请注意，某些通用组合工具可能无法按预期使用。

建立monadic（aka Kleisli）组合

让我们深入了解一下我们用于构成承诺提升函数的composeM函数：

const composeM = method => (...ms) => (
  ms.reduce((f, g) => x => g(x)[method](f))
);

隐藏在奇怪的reduce中的是函数组合的代数定义：f(g(x)).让我们更容易发现：

{
  // The algebraic definition of function composition:
  // (f ∘ g)(x) = f(g(x))
  const compose = (f, g) => x => f(g(x));
  const x = 20;    // The value
  const arr = [x]; // The container
  // Some functions to compose
  const g = n => n + 1;
  const f = n => n * 2;
  // Proof that .map() accomplishes function composition.
  // Chaining calls to map is function composition.
  trace('map composes')([
    arr.map(g).map(f),
    arr.map(compose(f, g))
  ]);
  // => [42], [42]
}

意味着我们可以编写一个通用的compose实用程序，它应该适用于所有提供.map方法的functor（例如，数组）：

const composeMap = (...ms) => (
  ms.reduce((f, g) => x => g(x).map(f))
);

这个只是稍微的描述下f(g(x))。给定类型a - > Functor(b)的任意数量的函数，迭代每个函数并将每个函数应用于其输入值x。.reduce方法采用具有两个输入值的函数：累加器（在本例中为f）和数组中的当前项（g）。

我们返回一个新函数x => g(x).map(f)，它在下一个应用程序中变为f。我们已经证明了x => g(x).map(f)相当于将compose(f, g)(x)提升到仿函数的上下文中。换句话说，它相当于将f(g(x))应用于容器中的值：在这种情况下，这会将合成应用于数组内的值。

性能警告：我不建议将其用于数组。以这种方式编写函数需要在整个数组上进行多次迭代（可能包含数十万个项目）。对于数组上的映射，首先组合简单的a - > b函数，然后在数组上映射一次，或者使用.reduce或传感器优化迭代。

对于数组数据上的同步，急切功能应用程序，这是过度的。但是，很多东西都是异步或懒惰的，许多函数需要处理混乱的事情，比如分支异常或空值。

这就是monad的用武之地.Monads可以依赖于依赖于组合链中先前的异步或分支动作的值。在这些情况下，你无法为简单的函数组合获得简单的值。你的monad返回动作采用a => Monad(b)而不是a> b的形式。

每当你有一个获取一些数据的函数，命中一个API，并返回一个相应的值，另一个获取该数据的函数，命中另一个API，并返回该数据的计算结果，你想要组成a => Monad(b)类型的函数。由于API调用是异步的，因此您需要将返回值包装为promise或observable。换句话说，这些函数的签名分别是 a -> Monad(b)和b -> Monad(c)。

函数组合的类型：g: a -> b, f: b -> c很容易，因为类型排队。h: a -> c只是a => f(g(a))。

函数组合的类型: g: a -> Monad(b), f: b -> Monad(c)有点难：h: a -> Monad(c)不只是a => f(g(a))因为f期望的是b,不是期望Monad(b)。

让我们更具体一点，组成一对异步函数，每个函数都返回一个promise：

{
  const label = 'Promise composition';
  const g = n => Promise.resolve(n + 1);
  const f = n => Promise.resolve(n * 2);
  const h = composePromises(f, g);
  h(20)
    .then(trace(label))
  ;
  // Promise composition: 42
}

我们如何编写composePromises以便正确记录结果？提示：你已经看过了。

还记得我们的composeMap函数吗？需要做的就是将.map调用更改为.then。 Promise.then基本上是异步的.map。

{
  const composePromises = (...ms) => (
    ms.reduce((f, g) => x => g(x).then(f))
  );
  const label = 'Promise composition';
  const g = n => Promise.resolve(n + 1);
  const f = n => Promise.resolve(n * 2);
  const h = composePromises(f, g);
  h(20)
    .then(trace(label))
  ;
  // Promise composition: 42
}

奇怪的是，当你点击第二个函数f（记住，在g之后的f），输入值是一个promise。它不是类型b，它是Promise(b)类型，但f类型为b，未包装。发生什么了？

在.then里面，有一个来自Promise(b) - > b的展开过程。该操作称为连接或展平。

可能已经注意到composeMap和composePromises几乎是相同的函数。这是可以处理两者的高阶函数的完美用例。让我们将链式方法混合到一个curried函数中，然后使用方括号表示法:

const composeM = method => (...ms) => (
  ms.reduce((f, g) => x => g(x)[method](f))
);

现在我们可以编写像这样的专用实现：

const composePromises = composeM('then');
const composeMap = composeM('map');
const composeFlatMap = composeM('flatMap');

Monad laws

在你开始构建之前，你需要知道他有三个定律：

  1. 左标识: unit(x).chain(f) ==== f(x)

  2. 右标识: m.chain(unit) ==== m

  3. 关联: m.chain(f).chain(g) ==== m.chain(x => f(x).chain(g))

The Identity Laws

monad是一个functor。他是类别之间的映射，A->B。映射是由箭头表示。除了我们在对象之间明确看到的箭头之外，类别中的每个对象也有一个回到自身的箭头。换句话说，对于类别中的每个对象X，存在箭头X - > X。该箭头称为标识箭头，通常将其绘制为从对象指向并循环回同一对象的小圆形箭头。

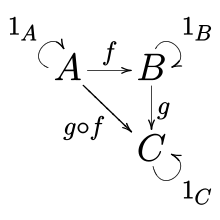
Associativity

关联性只意味着我们在写的时候放置括号的位置并不重要。例如，如果你加了个a + (b + c),等同于(a + b) + c 。函数组合也是这样：(f ∘ g) ∘ h = f ∘ (g ∘ h)

当看到合成运算符(chain)时，请考虑后面：

h(x).chain(x => g(x).chain(f)) ==== (h(x).chain(g)).chain(f)

Proving the Monad Laws

monad满足三个定律：

{ // Identity monad
  const Id = value => ({
    // Functor mapping
    // Preserve the wrapping for .map() by 
    // passing the mapped value into the type
    // lift:
    map: f => Id.of(f(value)),
    // Monad chaining
    // Discard one level of wrapping
    // by omitting the .of() type lift:
    chain: f => f(value),
    // Just a convenient way to inspect
    // the values:
    toString: () => `Id(${ value })`
  });
  // The type lift for this monad is just
  // a reference to the factory.
  Id.of = Id;
  const g = n => Id(n + 1);
  const f = n => Id(n * 2);
  // Left identity
  // unit(x).chain(f) ==== f(x)
  trace('Id monad left identity')([
    Id(x).chain(f),
    f(x)
  ]);
  // Id monad left identity: Id(40), Id(40)

  // Right identity
  // m.chain(unit) ==== m
  trace('Id monad right identity')([
    Id(x).chain(Id.of),
    Id(x)
  ]);
  // Id monad right identity: Id(20), Id(20)
  // Associativity
  // m.chain(f).chain(g) ====
  // m.chain(x => f(x).chain(g)  
  trace('Id monad associativity')([
    Id(x).chain(g).chain(f),
    Id(x).chain(x => g(x).chain(f))
  ]);
  // Id monad associativity: Id(42), Id(42)
}

结论

Monads是一种组合类型提升函数的方法：g: a => M(b), f: b => M(c)。为了这个，在应用f(n)之前必须将M(b)展开成b。

  • Functions map: a => b

  • Functors map with context: Functor(a) => Functor(b)

  • Monads flatten and map with context: Monad(Monad(a)) => Monad(b)

monad基于简单的对称性 - 将值包装到上下文中的方法，以及从上下文中解包值的方法：

  • Lift/Unit：从其他类型变成monad类型: a => M(a)

  • Flatten/Join: 返回到之前的类型M(a) => a

由于monad也是functor，他们也可以映射：

  • Map: Map with context preserved: M(a) -> M(b)

将flatten与map结合起来，你就可以获得用于提升功能的链 - 功能组合，也称为Kleisli组合：

  • FlatMap/Chain Flatten + map: M(M(a)) => M(b)

Monads必须满足三个法则（公理），统称为monad法则：

  • Left identity: unit(x).chain(f) ==== f(x)

  • Right identity: m.chain(unit) ==== m

  • Associativity: m.chain(f).chain(g) ==== m.chain(x => f(x).chain(g)

可能在每天JavaScript代码中遇到的monad示例包括promises和observables。Kleisli组合允许您编写数据流逻辑，而无需担心数据类型API的细节，也不必担心可能的副作用，条件分支或chain()操作中隐藏的展开计算的其他细节。

这使monad成为简化代码的强大工具。你不必理解或担心monad内部会发生什么，以获得monad可以提供的简化优势，但是现在你已经了解了更多关于内幕的内容，看看引擎盖下的内容并不是一件可怕的事情。

PreviouscurryNextmodule

Last updated