v8中推测性优化的介绍
TurboFan是什么?你可能需要了解下v8的基础
在JS Kongress上,我发表了一篇题为"TurboFan的故事" 演讲(查看幻灯片)。接下来,我想介绍一下V8的优化编译器TurboFan是如何工作的,以及V8如何将JavaScript转换成高度优化的机器码。对于演讲,我必须简短并省略一些细节。因此,我将利用这个机会来填补这些空白,特别是V8如何收集和使用分析信息来执行推测(推理)性优化。
概述
在我们深入了解TurboFan工作原理之前,我将简要介绍V8如何在高级别上运行。让我们来看看V8工作原理的简化分解(摘自我的同事Addy Osmani的"JavaScript启动性能"博客):
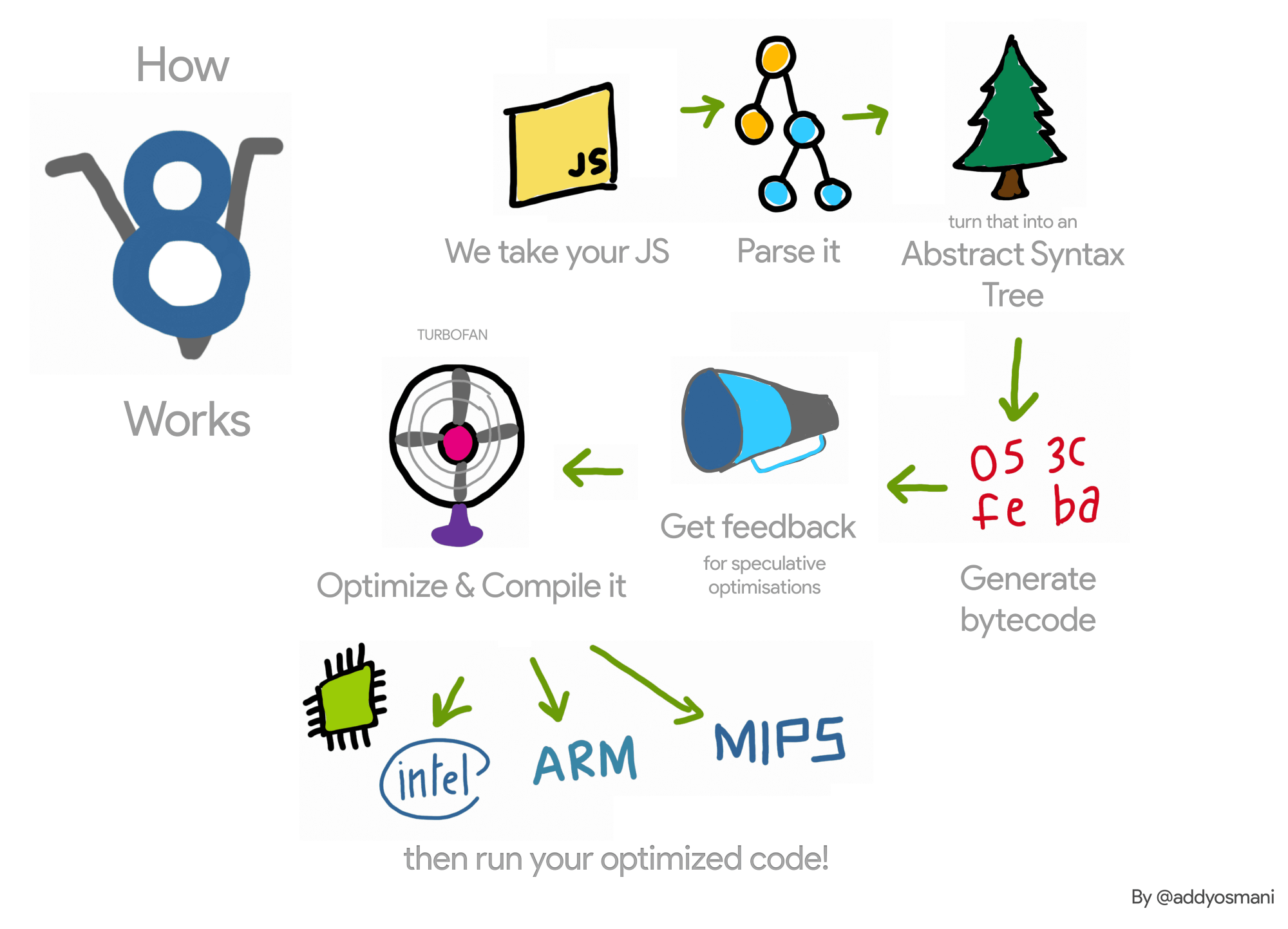
每当Chrome或Node.js必须执行某些JavaScript时,它会将源代码传递给V8。V8获取JavaScript源代码并将其提供给所谓的解析器(Parser),解析器为源代码创建抽象语法树(Abstract Syntax Tree AST) 表示。我的同事Marja Holtta发表了题为 "解析JavaScript——lazy解析比eager解析更好?" 的演讲包含了一些v8工作原理的细节。然后将AST传递给最近推出的Ignition Interpreter(Ignition解释器),它将变成一系列字节码。然后通过Ignition来执行这个字节码序列。
在执行过程中,Ignition收集有关某些操作输入的 分析信息或反馈 。其中一些反馈被Ignition本身用来加速字节码的后续解释。例如,对于诸如o.x之类的属性访问,其中o始终具有相同的形状(即,你总是为o传递值{x:v},其中v是String),我们缓存有关如何获取x值的信息。在后续执行相同的字节码时,我们不需要再次在o中搜索x。这里的底层机制称为内联缓存(inline cache, IC)。你可以我同事Vyacheslav Egorov的博客文章"单态是怎么回事?"中详细了解属性访问是如何工作的。
可能更重要的是——取决于你的工作量——由Ignition解释器收集的反馈被JavaScript的 Turbofan编译器使用,从而使用一种称为推测优化(Speculative Optimization)的技术生成高度优化的机器代码。在这里,优化编译器查看过去看到的值类型,并假设将来我们将看到相同类型的值。这使得TurboFan可以省去很多不需要处理的情况,这对于在最高性能下执行JavaScript是非常重要的。
基本的执行管道(Pipeline)
让我们考虑一下我演讲中示例的简化版本,只关注add函数以及V8如何执行它。
如果在Chrome DevTools控制台中运行它,会看到它输出预期结果3:
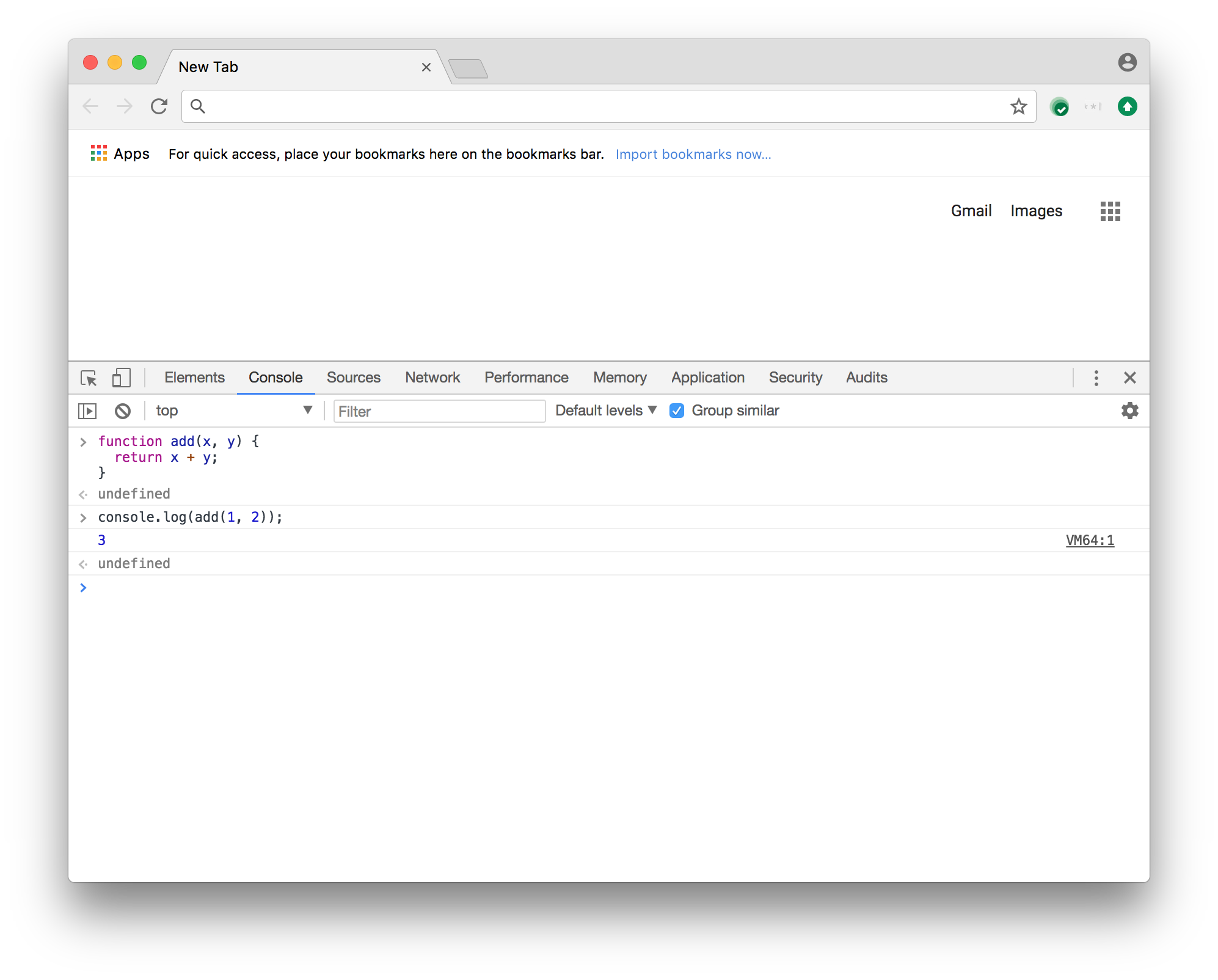
让我们来看看V8引擎下到底发生了什么来得到这些结果。我们将逐步执行函数add。如前所述,我们首先需要解析函数源代码并将其转换为抽象语法树(AST)。这是由Parser(解析器)完成的。你可以在d8 shell的Debug版本中使用--print-ast命令行标志查看V8内部生成的AST。
这种格式不是很容易理解,所以让我们想象它。
最初,add的函数文本被解析为树表示,其中一个子树用于参数声明,一个子树用于实际的函数体。在解析过程中,不可能知道哪些名称对应于程序中的哪些变量,这主要是由于JavaScript中有趣的var提升规则和eval,以及其他原因。因此,对于每个名称,解析器最初都会创建所谓的VAR PROXY节点。后续的作用域解析步骤将这些VAR PROXY节点连接到声明的VAR节点,或者将它们标记为全局查找或动态查找,这取决于解析器是否在周围的某个作用域中看到了eval表达式。
完成后,我们有一个完整的AST,其中包含从中生成可执行字节码的所有必要信息。然后将AST传递给BytecodeGenerator,它是Ignition解释器的一部分,它基于每个函数生成字节码。你仍然可以使用带有d8 shell(或带有node)的标志--print-bytecode来查看V8生成的字节码。
这告诉我们为函数add生成了一个新的字节码对象,它接受三个参数:隐式接收this,以及显式的形参x和y。该函数不需要任何局部变量(帧大小为零 -- Frame size 0),包含四个字节码序列:
为了解释这一点,我们首先需要了解解释器如何在高层次上工作。Ignition使用所谓的寄存器机器 -- register machine(与FullCodegen编译器中早期V8版本使用的堆栈机器方法形成对比)。它在解释器寄存器中保存其本地状态,其中一些映射到实际CPU寄存器,而其他寄存器映射到本机堆栈内存中的特定插槽。
特殊寄存器a0和a1对应于机器堆栈上函数的形参(在本例中,我们有两个形参)。形参是源代码中声明的参数,它可能与运行时传递给函数的实际参数数量不同。每个字节码的最后一个计算值通常保存在一个称为accumulator的特殊寄存器中,当前堆栈帧(stack frame)或激活记录(activation record)由stack pointer标识,program counter指向字节码中当前执行的指令。
StackCheck将stack pointer与一些已知的上限(实际上是一个下限,因为在V8支持的所有架构上堆栈都向下增长)进行比较。如果堆栈增长超过某个阈值,我们将中止该函数的执行并抛出一个RangeError,表示堆栈已溢出。Ldar a1将寄存器a1的值加载到accumulator寄存器中(名称表示 负载累加器寄存器(LoaD Accumulator Register))。Add a0, [0]从a0寄存器加载值并将其与accumulator寄存器中的值相加。然后将结果再次放入accumulator寄存器。注意,这里的加法也可以表示字符串连接,并且该操作可以根据操作数执行 任意JavaScript 。JavaScript中的+运算符非常复杂,很多人都在演讲中中试图说明它的复杂性。Emily Freeman最近在JS Kongress发表了题为 "JavaScript's"+""操作员和决策疲劳" 的演讲。Add操作符的[0]操作数指向一个反馈向量槽 ,在这里Ignition存储了关于我们在函数执行期间看到的值的分析信息。稍后我们将研究TurboFan如何优化该功能时再回头来讨论这个问题。Return结束当前函数的执行,并将控制权传回给调用方。返回的值是accumulator寄存器中的当前值。
我的同事Franziska Hinkelmann不久前写了一篇文章 "理解V8的字节码" ,它提供了一些关于V8字节码如何工作的额外见解。
推测优化
既然你已经大致了解了V8如何在baseline情况下执行JavaScript,那么现在就应该开始研究TurboFan如何适应这种情况,以及如何将JavaScript代码转换为高度优化的机器码。在JavaScript中,+操作符已经是一个非常复杂的操作,在它最终进行数字相加之前,必须进行大量检查。

目前还不清楚如何通过一些机器指令来实现这一点,从而达到最佳性能(与Java或c++代码相当)。这里的关键字是推测性优化 (Speculative Optimization),它利用对可能输入的假设。例如,当我们知道在x+y的情况下,x和y都是数字,我们不需要处理其中任何一个都是字符串的情况,或者更糟的情况——操作数可以是任意的javascript对象,我们需要首先在其上运行抽象操作ToPrimitive。

知道x和y都是数字也意味着我们可以排除可观察到的副作用——例如,我们知道它不会关计或写入文件或导航到另一个页面。另外我们知道操作不会抛出异常。这两项对于优化都很重要,因为优化编译器只有在确信表达式不会引起任何可见的副作用且不会引发异常的情况下才能消除表达式。
由于JavaScript的动态特性,我们通常直到运行时才知道值的准确类型,也就是说,仅仅通过查看源代码通常不可能知道操作输入的可能值。这就是为什么我们需要根据之前收集到的关于我们目前所看到的值的反馈进行推测,然后假设我们将来总是会看到类似的值。这可能听起来相当有限,但它已经证明可以很好地用于动态语言,如JavaScript。
在这种特殊情况下,我们收集有关输入操作数的信息以及+操作的结果值(Add字节码)。当我们使用TurboFan优化这段代码时,到目前为止我们只看到了数字,我们进行了检查,以检查x和y都是数字(在这种情况下,我们知道结果也将是数字)。如果这两种检查都失败了,我们就返回到解释字节码——一个称为反优化(Deoptimization)的过程。因此,TurboFan不需要担心+运算符的所有其他情况,甚至不需要发出机器码来处理这些情况,但是可以专注于数字的情况,这可以很好地转化为机器指令。
Ignition收集的反馈存储在所谓的反馈向量(以前称为类型反馈向量)中。这种特殊的数据结构与闭包连接,并包含存储不同类型反馈的槽,即位集、闭包或隐藏类,这取决于具体的内联缓存 (IC)。我的同事Michael Stanton今年早些时候在AmsterdamJS做了一个很好的演讲,题目是"V8以及它如何倾听你",其中详细解释了反馈向量的一些概念。闭包还会链接(link)到SharedFunctionInfo,其中包含关于函数的一些信息(如源位置、字节码、严格/非严格 模式等),并且还有一个到上下文的链接,其中包含函数的自由变量的值,并提供对全局对象(即<iframe>特定的数据结构)的访问。
对于add函数,反馈向量只有一个比较有趣的插槽(除了像调用计数插槽这样的常规插槽之外),这是一个BinaryOp插槽,其中二进制操作像+、-、*等。可以记录到目前为止所看到的输入和输出的反馈。在使用--allow-natives-syntax命令行标志(在d8的Debug构建中)运行时,可以使用专用的%DebugPrint()内在函数检查特定闭包的反馈向量内部的内容。
在d8中使用--allow-natives-syntax运行它,我们观察到:
我们可以看到调用计数为1(Invocation Count: 1),因为我们只运行了add函数一次。此外,还没有优化过的代码(由令人困惑的0来输出表示)。但是在反馈向量中只有一个槽,这是一个BinaryOp槽,它的当前反馈是SignedSmall。那是什么意思?到目前为止,引用反馈槽0的字节码Add只看到SignedSmall类型的输入,直到现在也只产生SignedSmall类型的输出。
但这个SignedSmall类型是什么?JavaScript没有这种的名称类型。这个名字来自于V8中的一个优化,当表示小的带符号整数值时,这个整数值在程序中频繁出现,需要特殊处理(其他JavaScript引擎也有类似的优化)。
徘徊: 值得表示
让我们简要地研究一下JavaScript值在V8中是如何表示的,以便更好地理解底层概念。V8通常使用一种称为指针标记的技术来表示值。我们处理的大多数值都存在于JavaScript堆中,并且必须由垃圾收集器(GC)管理。但对于某些值,总是将它们分配到内存中太昂贵了。特别是对于经常用作数组索引和临时计算结果的小整数值。
在V8中,我们有两种可能的标记表示: Smi(Small Integer的缩写)和HeapObject,它指向托管堆中的内存。我们利用了这样一个事实,即所有分配的对象都在字边界上对齐(64位或32位取决于体系结构),这意味着2或3个最低有效位始终为零。我们使用最小有效位来区分HeapObject(位为1)和Smi(位为0)。对于64位体系结构上的Smi,最低有效的32位实际上都是零,并且签名的32位值存储在单词的上半部分。这允许使用一条机器指令有效地访问内存中的32位值,而不必加载和移动该值,而且还因为32位算术对于JavaScript中的按位运算很常见。在32位体系结构上,Smi表示法将最低有效位设置为0,并且将一个有签名的31位值向左移动一个存储在单词的31位上的值。
反馈格
SignedSmall反馈类型引用所有具有Smi表示的值。对于Add操作,这意味着到目前为止,它只看到输入表示为Smi,而生成的所有输出也可以表示为Smi(即值没有超出可能的32位整数值的范围)。让我们检查如果我们还使用其他不是表示为Smi的数字来调用add会发生什么。
在d8中使用--allow-natives-syntax再次运行它,我们观察到:
首先,我们看到调用计数现在是2,因为我们运行了两次函数。然后我们看到BinaryOp槽值改为Number,这表明我们已经看到了加法的任意数字(即非整数值)。对于加法,有一个反馈的可能状态的格子,大致是这样的:
反馈以
None开始,这表明到目前为止我们还没有看到任何东西,所以我们什么都不知道。Any状态表示我们已经看到了不兼容的输入或输出的组合。因此,Any状态表示Add被认为是多态的。相反,其余的状态表明Add是单态的,因为它只看到并产生了有些相同的值。
SignedSmall表示所有值都是小整数(签名的32位或31位,具体取决于体系结构的字大小),并且所有值都表示为Smi。Number表示所有值都是常规数字(包括SignedSmall)。NumberOrOddball包含Number加上undefined,null,true和false的所有值。String表示两个输入都是字符串值。BigInt意味着两个输入都是BigInts,有关详细信息,请参阅当前的第2阶段提案。
需要注意的是,反馈只能在这个格子中进行。不可能再回去了。如果我们回到之前,那么我们就有可能进入一个所谓的反优化循环(deoptimization loop),在这个循环中,优化编译器消耗反馈,当它看到与反馈不一致的值时,就从优化代码(返回到解释器)中退出。下次函数变热时,我们将再次优化它。所以如果我们不在格子上继续,那么TurboFan将会再次产生同样的代码,这意味着它将会在同样的输入上再次跳出来(退出)。因此,引擎将忙于优化和反优化代码,而不是高速运行JavaScript代码。
优化管道
既然我们已经知道了Ignition如何为add函数收集反馈,那么让我们看看TurboFan如何利用这些反馈生成最小的代码。我将使用特殊的内部函数%OptimizeFunctionOnNextCall()在特定的时间点触发V8中函数的优化。我们经常使用这些内部特性来编写测试,以一种非常特殊的方式对引擎施加压测。
在这里,我们通过传递两个整数值来显式地使用SignedSmall反馈来预热x+y,这两个整数值的和也符合小整数范围。然后我们告诉V8它应该在下次调用时优化函数add(使用TurboFan),最后我们调用add,它会触发TurboFan,然后运行生成的机器代码。
TurboFan获取先前为add生成的字节码,并从add的FeedbackVector中提取相关反馈。它将其转换为图形表示,并将图形传递到前端,优化和后端阶段的各个阶段。我不打算在这里讨论传递的细节,这可以是一篇单独的博客文章(或一系列单独的博客文章)的主题。相反,我们将查看生成的机器代码,并了解推测优化的工作原理。你可以通过将--print-opt-code标志传递给d8来查看TurboFan生成的代码。
这是由TurboFan生成的x64机器码,带有来自我的注释,省略了一些无关紧要的技术细节(即对Deoptimizer的确切调用顺序)。那么让我们看看代码的作用:
prologue检查代码对象是否仍然有效,或者是否更改了某些条件,从而要求我们丢弃代码对象。这是我的实习生Juliana Franco最近在她的"Internship on Laziness"中介绍的。一旦我们知道代码仍然有效,我们构建堆栈帧并检查堆栈上是否有足够的空间来执行代码。
然后我们从函数体开始。我们从堆栈中加载参数x和y的值(相对于rbp中的帧指针),并检查两个值是否都有Smi表示(因为+的反馈表示两个输入到目前为止一直都是Smi)。这是通过测试最小有效位来完成的。一旦我们知道它们都被表示为Smi,我们需要将它们转换为32位表示,这是通过将值向右移位32位来完成的。
如果x或y不是Smi,则优化代码的执行立即中止,并且Deoptimizer(反优化)在Add之前在解释器中恢复函数的状态。
注:我们也可以在这里对Smi表示进行加法;这就是我们之前优化编译器Crankshaft所做的。这样可以省去我们的转变,但是目前TurboFan没有一个好的启发式方法来决定是否在Smi上进行操作是有益的,这并不总是理想的选择,而且高度依赖于使用此操作的上下文。
然后我们继续对输入执行整数加法。我们需要显式地测试溢出,因为加法的结果可能超出32位整数的范围,在这种情况下,我们需要返回解释器,解释器将在Add上学习Number反馈。最后,通过将签名的32位值向上移动32位,将结果转换回Smi表示,然后返回累加器寄存器rax中的值。
如前所述,对于这种情况,这还不是完美的代码,因为在这里,直接对Smi表示执行加法是有益的,而不是使用Word32I,这将为我们节省三条移位指令。但是,即使撇开这个次要方面不谈,你也可以看到生成的代码经过了高度优化,并且专门用于分析反馈。它甚至没有尝试在这里处理其他数字,字符串,大整数或任意JavaScript对象,而只关注我们到目前为止看到的那种值。这是许多JavaScript应用程序达到性能峰值的 关键因素 。
取得进展
那么,如果你突然改变主意,想要添加数字呢?让我们把这个例子改成这样:
使用--allow-natives-syntax和--trace-deopt运行它,我们会观察到以下内容:
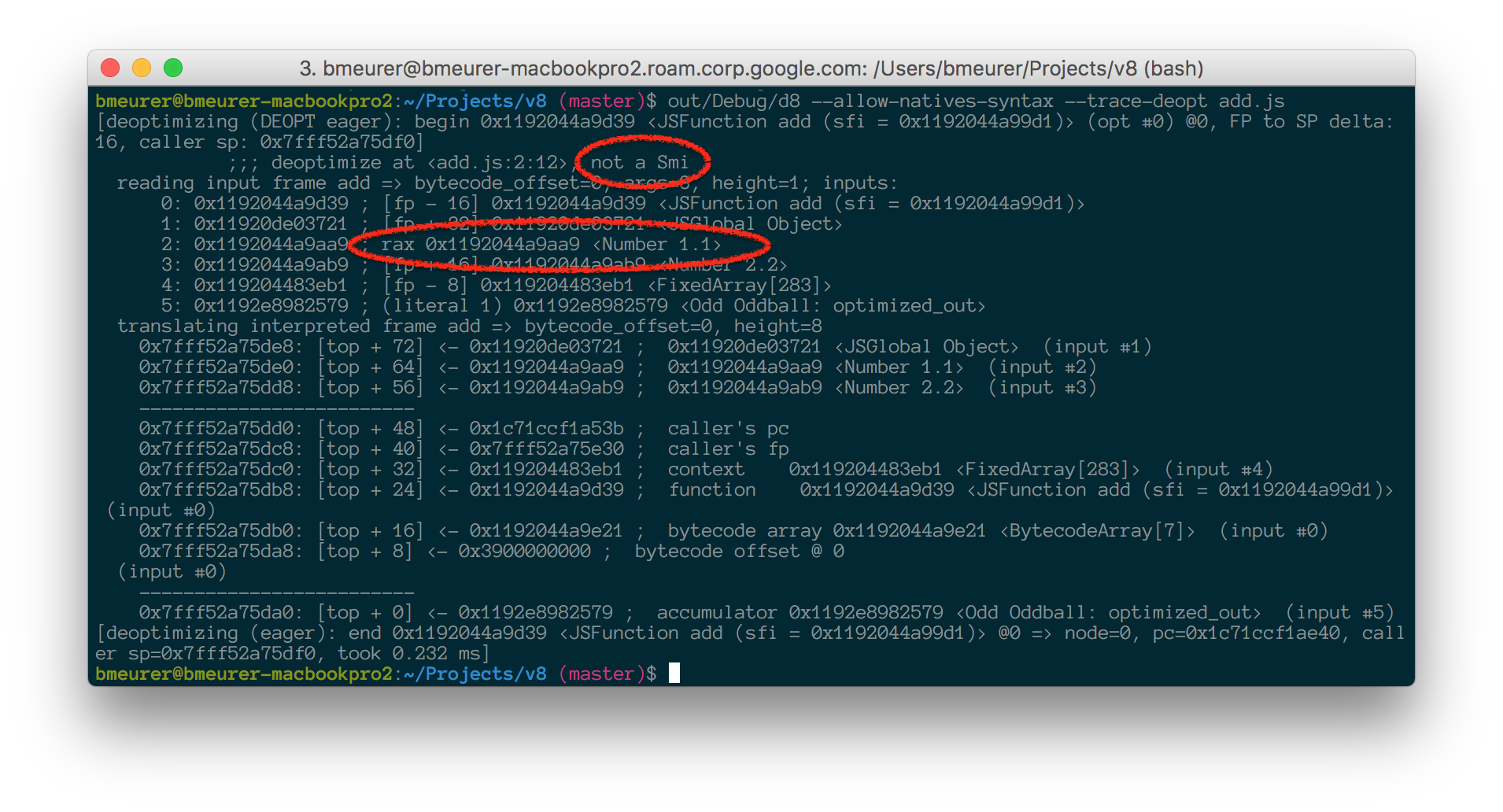
这有很多令人困惑的输出。但是让我们提取重要的部分。首先,我们打印出一个我们必须去优化的原因,在这种情况下它not a Smi,这意味着我们假设某个值是Smi,但现在我们看到了一个HeapObject。实际上它是rax中的值,它应该是一个Smi,但它的数字是1.1。所以我们在第一次检查x参数时失败了,我们需要去反优化以返回解释字节码。这是一篇单独文章的主题。
Takeaway
希望你喜欢这篇关于V8中推测性优化的文章,以及它如何帮助我们达到JavaScript应用程序的最高性能。不要过分担心这些细节。在JavaScript中编写应用程序时,请关注应用程序设计,并确保使用适当的数据结构和算法。编写惯用的JavaScript,让我们转而关注JavaScript性能的低级别。如果你发现有些东西太慢了,而且不应该太慢,请提交一个bug报告,这样我们就有机会研究一下。
译者总结
Parser解析成AST(抽象语法🌲),这个AST有个子🌲用于参数声明,一个子树是函数体,会执行一些标记,这就成为了生成字节码的必要信息,有了这些信息,就可以把AST传递给BytecodeGenerator(Ignition解释器的一部分)生成字节码。
Turbofan会对代码进行推测优化(在无副作用和不会抛错的情况下),会对代码进行假设。(假设失败了,那就返回到解析字节码,这个是反优化(deoptimization))。比如Turbofan假设输入的参数都是smi(Small Integer),参数累加的结果也是smi,但是结果不是一个smi,你可能看到了一个HeapObject,那么就是认为失败了,并反优化。(这个只是一个抽象的概念,譬如作者所说的,可以另开一个博客了)
Last updated